이상현상과 함수종속

정규화의 개념과 이상 현상

• 이상(anomaly) 현상
  불필요한 데이터 중복으로 인해 릴레이션에 대한 데이터 삽입/수정/삭제 연산을 수행할 때 발생할 수 있는 부작용
• 정규화
  이상 현상을 제거하면서 데이터베이스를 올바르게 설계해 나가는 과정

  이상 현상의 종류

  삽입 이상

  릴레이션에 새 데이터를 삽입하기 위해 불필요한 데이터도 함께 삽입해야 하는 문제

고객아이디	이벤트번호	당첨여부	고객이름	등급
A	E01	Y	영희	gold
B	NULL	NULL	철수	gold

B고객의 정보를 삽입하려고 할 때 B고객이 이벤트에 참여하지 않아 키값이 NULL일 때 삽입이 불가능하다.

갱신 이상

릴레이션의 중복된 튜플 중 일부만 수정하여 데이터가 불일치하게 되는 모순의 문제

고객아이디	이벤트번호	당첨여부	고객이름	등급
A	E01	Y	영희	vip
A	E07	N	영희	gold
A	E09	Y	영희	gold

gold에서 vip로 등급이 상승했지만 나머지 2개의 값을 변경해주지 않아 데이터가 불일치하게 된다. 튜플이 불필요하게 중복되어 생기는 문제다.

삭제 이상

릴레이션에서 튜플을 삭제하면 꼭 필요한 데이터까지 함께 삭제되는 데이터 손실의 문제

고객아이디	이벤트번호	당첨여부	고객이름	등급
A	E01	Y	영희	vip
B	E07	N	철수	gold

B고객이 이벤트참여를 취소하는 경우에 이벤트번호 뿐만이 아니라 다른 필요한 정보들까지 함께 삭제된다.

정규화

• 이상 현상이 발생하지 않도록 릴레이션을 관련 있는 속성들로만 구성하기 위해 릴레이션을 분해(decomposition)하는 과정
• 함수적 종속성을 판단하여 정규화를 수행한다.

함수적 종속성(FD - Functional Dependency)

• 속성들 간의 관련성을 말한다.
• 함수 종속성을 이용하여 릴레이션을 연관성이 있는 속성들로만 구성되도록 분해하여 이상 현상이 발생하지 않는 바람직한 릴레이션으로 만들어 나가는 과정이 정규화다.

함수 종속

• “x가 y를 함수적으로 결정한다.”
  • 릴레이션 내의 모든 튜플을 대상으로 하나의 x값에 대한 y값이 항상 하나다.
  • x와 y는 하나의 릴레이션을 구성하는 속성들의 부분 집합이다.
  • “y가 x에 함수적으로 종속되어 있다”와 같은 의미다.
  • x -> y로 표현한다.(x는 결정자, y는 종속자)

함수 종속 관계 판단 예1

고객아이디	고객이름	등급
A	영희	vip
B	철수	gold
C	민수	gold

고객아이디 -> 고객이름, 고객아이디 -> 등급
또는
고객아이디 -> {고객이름, 등급}

고객이름 -> 등급 은 될 수 없다. 고객이름이 중복될 수도 있기 때문이다. 각 고객아이디 속성 값에 대응되는 고객이름 속성과 등급 속성 값은 단 하나여야 한다.

• 함수 종속 다이어그램
  함수 종속 관계를 도식화하여 표현한 것이다.
  

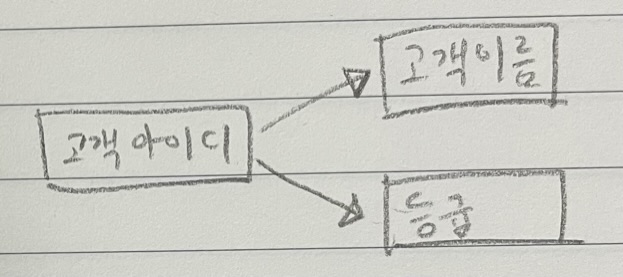
함수 종속 관계 판단 예2

고객아이디	이벤트번호	당첨여부	고객이름
A	E01	Y	영희
A	E07	N	영희
A	E09	Y	영희

고객아이디 -> 고객이름
{고객아이디, 이번트번호} -> 당첨여부
{고객아이디, 이벤트번호} -> 고객이름

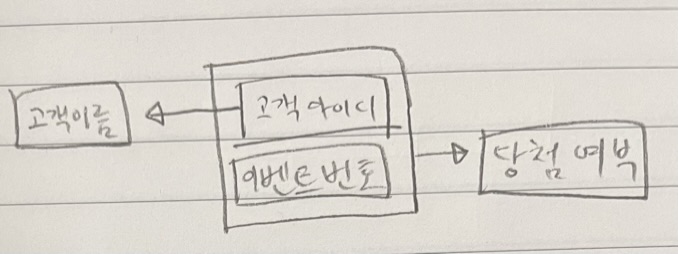
고객이름은 {고객아이디, 이벤트번호}의 일부분인 고객아이디에 종속되어 있다.
-> 고객이름은 {고객아이디, 이벤트번호}에 부분 함수 종속된다.

함수 종속 관계 판단 시 유의 사항

• 속성 자체의 특성과 의미를 기반으로 함수 종속성을 판단해야 한다.
  속성 값은 계속 변할 수 있으므로 현재 릴레이션에 포함된 속성 값만으로 판단 하면 안된다.

고객아이디	고객이름	등급
A	영희	vip
B	철수	gold

현재에서는 고객이름 영희는 등급 vip하나를 가져 함수 종속 관계가 있다고 할 수도 있지만 나중에 동명이인의 영희가 등급 silver를 가진다면 고객이름과 등급간에 함수 종속 관계가 존재하지 않게 된다.

• 일반적으로 기본키와 후보키는 릴레이션의 다른 모든 속성들을 함수적으로 결정한다.
• 기본키나 후보키가 아니어도 다른 속성 값을 유일하게 결정하는 속성은 함수 종속 관계에서 결정자가 될 수 있다.

완전 함수 종속(FFD - Full Functional Dependency)

• 릴레이션에서 속성 집합 y가 속성 집합 x에 함수적으로 종속되어 있지만, 속정 집합 x의 전체가 아닌 일부분에는 종속되지 않음을 의미한다.
• 일반적으로 함수 종속은 완전 함수 종속을 의미한다.
• 예)

고객아이디	이벤트번호	당첨여부	고객이름
A	E01	Y	영희
A	E07	N	영희
A	E09	Y	영희

당첨여부는 {고객아이디, 이벤트번호}에 완전 함수 종속된다.
고객아이디, 이벤트번호를 조합해야 종속 관계가 생긴다.

부분 함수 종속(PFD - Partial Functional Dependency)

• 릴레이션에서 속성 집합 y가 속성 집합 x의 전체가 아닌 일부분에도 함수적으로 종속됨을 의미한다.
• 예)

고객아이디	이벤트번호	당첨여부	고객이름
A	E01	Y	영희
A	E07	N	영희
A	E09	Y	영희

고객이름은 {고객아이디, 이벤트번호}에 부분 함수 종속된다.
고객아이디, 이벤트번호 모두를 조합해도 되고 둘 중 하나만으로도 종속 관계가 있을 수 있다.

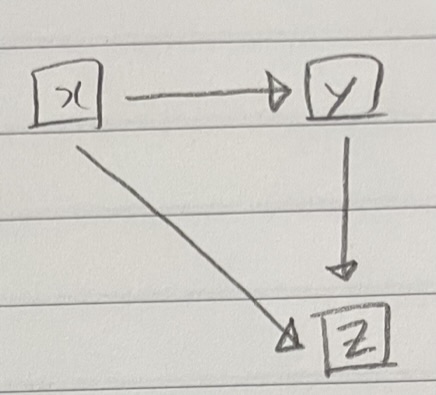
이행적 함수 종속(transitive FD)

릴레이션을 구성하는 세 개의 속성 집합 x, y, z에 대해 함수 종속 관계 x -> y와 y -> z가 존재하면 논리적으로 x -> z가 성립되는데, 이것을 z가 x에 이행적으로 함수 종속되었다고 한다.

고려할 필요가 없는 함수 종속 관계

결정자와 종속자가 같거나, 결정자가 종속자를 포함하는 것처럼 당연한 함수 종속 관계는 고려하지 않는다.

고객아이디 -> 고객아이디
{고객아이디, 이벤트번호} -> 이벤트번호